FERENCI TAMÁS válasza

A Covid járvány tanulságairól tettünk fel 7 nyílt kérdést.

Aug 12, 2024

Előszó:

2024. július 10-én nyílt kérdéseket küldtünk el. A címzettek között szerepelt Kásler Miklós, Müller Cecília, Oroszi Beatrix, Szlávik János, Nagy Eszter, Merkely Béla, Kemenesi Gábor, Letoha Tamás, Ferenci Tamás, Duda Ernő, Boldogkői Zsolt, Tamasi József, Gődény György, a koronavírus kisokos, a KOVIDők, Tauber Zsófia, Bíró Éva, a Qubit.hu, a lakmusz.hu és az orvosokatisztanlatasert.hu. Kíváncsaik voltunk a véleményükre, és arra, mi alapján alakult ki bennük.

A válaszokat először is változtatások nélkül közöljük a honlapon, érkezési sorrendben. (Ez természetesen nem azt jelenti, hogy mindenben egyetértenénk az itt leírtakkal.)

Ezek után megkeressük a válaszadókat, hogy a rádióadásban beszéljünk velük, feltegyük a bennünk felmerült további kérdéseket. Majd a válaszokból és beszélgetésekről témákra bontva összefoglalókat is készítünk, amit közzéteszünk itt a honlapon.

Ferenci Tamás válaszai

Ferenci Tamás klinikai biostatisztikus, orvosbiológiai mérnök. A leírtak teljes egészében a magánvéleményét képviselik. A Covid témájában többször nyilatkozó szakértő (pl. itt, itt és itt), valamint több meghívásunkat is elfogadta a rádióadásunkba (itt és itt).

`2.` Ön mit gondol: a Covid oltásoknak több az előnye, mint a hátránya?

Én azt gondolom, hogy erre a kérdésre ebben a formában nem lehet válaszolni.

Ezt csak akkor tudnánk megtenni, ha mind az előny, mind a hátrány valamiféle állandó érték lenne, és a feladat pusztán annyi volna, hogy megítéljük, hogy a kettő közül melyik a nagyobb. Ez esetben ez valóban egy igen/nem típusú kérdés lenne, csakhogy a valóság ennél jóval bonyolultabb:

Egy oltás esetében az előny egy jövőbeli fertőződés megelőzése, vagy, ha az nem is érhető el, a lefolyás enyhítése és így a következményeinek (különösen: súlyos kimenet, halálozás) megelőzése. A probléma az, hogy innentől kezdve az előny attól is függ, hogy magának a megfertőződésnek, a súlyos kimenetnek mekkora a kockázata – ez viszont függ attól, hogy milyen emberről beszélünk, hogy csak a legkézenfekvőbbet említsem, az életkortól. Ennek a kérdésnek semmi köze az oltás jóságához; amikor azt mondom, hogy egy 20 évesnek átlagosan kisebb az előnye az oltásból, mint egy 90 évesnek, az nem azért van, mert azt gondolom, hogy az oltás kevésbé működik 20 évesen, mint 90 évesen, hanem azért, mert 20 évesen az oltás nélküli kockázat is kisebb. Ugyanígy számíthatnak a társbetegségek, a kórelőzmény, a szocioökonómiai státusz vagy épp a meglevő immunitás – minden, ami befolyásolja az oltás nélküli kockázatot.
A második probléma az előny kapcsán, hogy valójában nem csak az nem állandó, hogy a megfertőződés esetén mekkora a kockázat, amit fent részleteztem, hanem maga a megfertőződés kockázata sem állandó. Egy tomboló járvány kellős közepén sokkal nagyobb az oltás előnye, mint amikor nem, vagy alig cirkulál a vírus.
Végezetül pedig valójában a másik serpenyő, az oltás hátránya sem feltétlenül állandó. Jól ismert például, hogy az oltás utáni szívizomgyulladás kockázata függ a nemtől (férfiakban nagyobb).

Ezekből fakadóan fogalmaztam úgy, hogy a kérdésre véleményem szerint a fenti formában nem lehet válaszolni, hiszen csak olyan jellegű válaszok adhatóak mint hogy „most egy éppen kitörő járványhullámban, kevés meglevő immunitással, a lakosság abszolút túlnyomó többsége számára elsöprően több az oltás előnye mint hátránya” vagy, hogy „most, érdemleges járvány nélkül és jelentős meglevő immunitás mellett az egészséges fiatalok esetében több az oltás hátránya mint előnye” vagy, hogy „most, egy kezdődő téli szezon előtt még jelentős meglevő immunitás mellett is több az oltás előnye mint a hátránya krónikus betegek esetében” stb. stb. Hogy a milliónyi hasonló állítás közül éppen melyik igaz, azt nem fogom tudni itt megmondani (pláne úgy, hogy ez elsősorban nem biostatisztikai kérdés), én most pusztán arra kívántam felhívni a figyelmet, hogy szerintem a kérdést már feltenni is csak ebben a formában van értelme [1].

Lábjegyzet:
[1]. Joggal merül fel, hogy akkor a népegészségügyi szervek miért nem a fenti három pontot, meg ilyen mondatokat nyomtatnak a plakátokra. Én a szívem szerint ezt tenném, de ettől a gondolattól meg a kommunikációhoz értő barátaim kapnak agyvérzést, vagy fordulnak le röhögve a székről, mert ők azt mondják, hogy egyoldalas kisesszék és ilyen mondatok plakátra nyomtatása nem alaposságot és gondosságot, hanem simán bizonytalankodást sugallna, ami nem szerencsés, pláne nem egy járvány kellős közepén. Ebben a kérdésben nem tudok igazságot tenni.

2.1. Ismer olyan tanulmányokat, amik bemutatják a Covid oltások előnyeinek (pl: megelőzött Covid halálesetek) és hátrányainak (pl: oltásmellékhatás miatti halálesetek) összehasonlítását? Minket főleg az új típusú, ezelőtt még soha nem használt módszerekkel dolgozó oltásokkal kapcsolatosak érdekelnek (pl.: Pfizer-BioNTech és Moderna mRNS oltások).

Igen, ismerek ilyet, és ha lehetek szerénytelen, akkor elsőként rögtön említeném a sajátomat:

https://github.com/tamas-ferenci/AKockazatHaszonMerlegelesEgyPeldajarol

Ezen kívül számos ilyen lelhető fel az irodalomban, e pillanatban a PubMed, az orvosi cikkek legáltalánosabban használt, bárki számára nyilvános keresője több száz találatot ad [2]. Ezek között természetesen biztosan van irreleváns [3], a relevánsak között is biztosan van olyan, amit meg lehet kérdőjelezni, de a tényt, hogy léteznek ilyen tanulmányok, úgy gondolom, nem.

Lábjegyzet:
[2]. Például az egyik legkézenfekvőbb keresőkifejezéssel e sorok írásának pillanatában 494 találatot kapunk. A keresést – továbbra is a legegyszerűbb módon – az mRNS-vakcinákra szűkítve is bőven több mint száz találatunk van.
[3]. De nem mindegyik ilyen, bizonyságul pár releváns tanulmány:
Patrick R Funk, Osman N Yogurtcu, Richard A Forshee, Steve A Anderson, Peter W Marks, Hong Yang. Beneft-risk assessment of COVID-19 vaccine, mRNA (Comirnaty) for age 16-29 years. Vaccine. 2022 Apr 26;40(19):2781-2789.
Jonathan Fix, T Christopher Mast, Katherine Smith, Nicole Baker. Beneft-risk assessment for the Novavax COVID-19 vaccine (NVX-CoV2373). Vaccine. 2024 Apr 2;42(9):2161-2165.
Taito Kitano, Daniel A Salmon, Matthew Z Dudley, David A Thompson, Lilly Engineer. Beneft-Risk Assessment of mRNA COVID-19 Vaccines in Children Aged 6 Months to 4 Years in the Omicron Era. J Pediatric Infect Dis Soc. 2024 Feb 26;13(2):129-135.
Osman N Yogurtcu, Patrick R Funk, Richard A Forshee, Steven A Anderson, Peter W Marks, Hong Yang. Beneft-risk assessment of Covid-19 vaccine, MRNA (MRNA-1273) for males age 18-64 years. Vaccine X. 2023 Aug:14:100325.
Megan Wallace, Hannah G Rosenblum, Danielle L Moulia, Karen R Broder, Tom T Shimabukuro, Christopher A Taylor et al. A summary of the Advisory Committee for Immunization Practices (ACIP) use of a beneft-risk assessment framework during the frst year of COVID-19 vaccine administration in the United States. Vaccine. 2023 Oct 20;41(44):6456-6467.
Taito Kitano, David A Thompson, Lilly Engineer, Matthew Z Dudley, Daniel A Salmon. Risk and Benefit of mRNA COVID-19 Vaccines for the Omicron Variant by Age, Sex, and Presence of Comorbidity: A Quality-Adjusted Life Years Analysis. Am J Epidemiol. 2023 Jul 7;192(7):1137-1147.

2.2.1. Ön szerint az oltottak vagy az oltatlanok haltak-e meg nagyobb eséllyel 2021 és 2023 között?

Az általam ismert hazai [4] és nemzetközi (angol [5], cseh [6]) adatok alapján a válasz egységesen és egyöntetűen az, hogy az oltatlanok.

Nagyon fontos azonban ehhez az eredményhez azonnal hozzátenni, hogy ez – önmagában – nem bizonyítja, pláne erősen, hogy az oltások hatásosak. A probléma az, hogy az oltott és oltatlan csoportok nem csak az oltás tényében térnek el – innen kezdve, ha találunk is különbséget köztük a kimenetben (jelen esetben a halálozásban), nem tudhatjuk, hogy az mi miatt van: az oltottság miatt, az oltottsággal együtt járó egyéb eltérések miatt, vagy ezek valamilyen keveréke miatt? Képzeljük el, egyelőre csak gondolatkísérletként, most még minden tényadat nélkül, hogy az oltás hatástalan, de az oltottak között kevesebb a cukorbeteg, miközben a cukorbetegeknek rosszabb a túlélése önmagában a betegségükből fakadóan. Mit fogunk ebben az esetben egy egyszerű oltott/oltatlan összehasonlítással kimutatni? Természetesen azt, hogy az oltás hatásos! Miközben nem az, és ez most biztos, hiszen ez egy gondolatkísérlet volt, amit így konstruáltunk meg. Akár még az is lehet, hogy az oltás egyenesen káros, de az oltottaknak mégis jobb a túlélése. (Ha annyival kevesebb köztük a cukorbeteg, hogy ennek a jótékony hatása nagyobb, mint az oltás káros hatása.) Segíthet megérteni a dolgot, ha így fogalmazzuk meg: bár az oltottaknak jobb a túlélése, de az oltás mégis káros, és ez azért nem ellentmondás, mert ha nem kaptak volna oltást, akkor még jobb lett volna a túlélésük! Ez a megfogalmazás mutatja, hogy mi a probléma magva: az, hogy nem ismerjük az alternatív, „mi lett volna ha” forgatókönyvet, nem tudjuk mi történt volna, ha nem kaptak volna oltást. A dolog természetesen fordítva is működik: ha az oltás hatásos, de az oltottak között több a cukorbeteg, akkor előfordulhat, hogy az oltottak túlélése rosszabb, azaz azt hisszük az egyszerű vizsgálatban, hogy az oltás hatástalan, vagy egyenesen káros – miközben a valóságban hatásos. Itt is segít az előbbihez hasonló megfogalmazás: az oltottak túlélése ugyan rosszabb, de az oltás mégis hatásos, mert oltás híján még rosszabb lett volna!

Ez egy példa arra az általános jelenségre, amit magyarban is gyakran használt angol szóval confounding-nak szoktak hívni: ha több szempontból eltérő csoportok hasonlítunk össze, akkor hiába is találunk különbséget, nem fogjuk tudni, hogy az melyik eltérés miatt van. A kérdés iránt mélyebben érdeklődőknek merem ajánlani a témát hosszabban – de reményeim szerint érthetően – tárgyaló írásomat, mely elérhető a

https://tamas-ferenci.github.io/FerenciTamas_AzOrvosiMegismeresModszertanaEsAzOrvosiKutatasokKritikusErtekelese/

címen.

A confounding jelenléte miatt a fentihez hasonló, megfigyeléses vizsgálatoknál [7], ahol nincs garantálva, hogy az oltott és az oltatlan csoportok csak az oltás tényében térnek el, mindig óvatosan kell eljárni. Mindez nem csak elméleti aggodalom, hanem aláhúzzák a tényadatok is.

Az egyik effektus, hogy az oltottak elképzelhető, hogy bizonyos szempontokból egészségesebbek. Ennek az egyik kézenfekvő példája, hogy egy autóbaleset másnapján, az épp intenzíven kómában fekvő beteget jó eséllyel nem fogják beoltani, ezért az oltottak csoportja mentes a „tegnap gázolta el őket az autó” – extrém magas halálozási kockázatú – halmaztól. De lehet kevésbé drasztikus példákra is gondolni, mondjuk, hogy a mobilisabb, vagy egészségtudatosabb lakosok inkább beoltatják magukat; mindezeket szoktuk összefoglaló néven egészséges oltott hatásnak nevezni. Ha ezzel nem törődünk, akkor felülbecsüljük az oltás hatását, beleértve azt a lehetőséget is, hogy egy hatástalan, vagy akár káros oltást hatásosnak minősítünk. (Mint a fenti első példa: ha az oltottak egészségesebbek, akkor pusztán ebből fakadóan is jobb a kimenetük, ezért a jobb túlélés nem biztos, hogy az oltás pozitív hatása, akár még az is lehet, hogy annak ellenére történt.) A másik effektus, hogy az oltottak elképzelhető, hogy bizonyos szempontokból kevésbé egészségesek. Ezt a koronavírus-járvány után senkinek nem kell magyarázni, mindenki jól emlékszik, hogy kik kaptak elsők között oltást, kiknek javasolták sokkal erősebben: az idősebbeknek, a krónikus betegeknek. Erre még szó szerint tényadatot is lehet hozni, Magyarországról is: Pálinkás és mtsa korábban már idézett cikke megadja [8] az oltott és oltatlan csoportok alapvető adatait. Pár megállapítást kiragadnék példaként: a teljesen oltottak majdnem 10 évvel (!) idősebbek átlagosan mint az oltatlanok, kétszer annyi köztük a cukorbeteg, kétszer annyi a magasvérnyomás-beteg, több mint kétszer annyi köztük olyan, aki rákosként kapott oltást. Ezt szokták indikáció általi confounding-nak nevezni, és pont az előző hatás ellentétéhez vezet: ha ezzel nem törődünk, akkor alábecsüljük az oltás hatását, beleértve azt a lehetőséget is, hogy egy hatásos oltást hatástalannak, vagy akár károsnak minősítünk. (Mint a fenti második példa: ha az oltottak betegebbek, akkor pusztán ebből fakadóan is rosszabb a kimenetük, ezért a rosszabb túlélés nem biztos, hogy az oltás negatív hatása, akár még az is lehet, hogy annak ellenére történt.)

Fontos kiemelni, hogy nem arról van szó, hogy az egyik hatás van jelen vagy a másik: mindkettő jelen van, egyszerre, különböző komponenseik különböző mértékben. A megfigyeléses adatok ilyen zűrösek; anélkül, hogy az ilyen és ehhez hasonló különbségekre megpróbálnánk finoman kontrollálni, ahogy azt a rendes kutatásokban teszik, gyakorlatilag kizárt, hogy értelmes következtetést tudjunk levonni. Újra hangsúlyozom, hogy ez mindkét irányban igaz, tehát a legegyszerűbb ha azt mondjuk: szinte mindegy is, hogy mi a válasz a feltett kérdésre, abból nem, vagy csak rendkívül bizonytalanul lehet következtetni az oltás hatásosságára.

Lábjegyzet:
[4]. Pálinkás és mtsa kutatása sajnos csak egy nagyon rövid időszakot (2021 áprilisa és júniusa közti három hónap) vizsgál, de ebben az oltatlanok halálozása 8,01 /100 ezer fő/év volt, az oltottaké 4,64 /100 ezer fő/év. Anita Pálinkás, János Sándor. Effectiveness of COVID-19 Vaccination in Preventing All-Cause Mortality among Adults during the Third Wave of the Epidemic in Hungary: Nationwide Retrospective Cohort Study. Vaccines (Basel). 2022 Jun 24;10(7):1009.
[5]. Az adatok elérhetőek itt, vizualizációt magam is fogok közölni a következő pontban.
[6]. Az adatok elérhetőek itt, egy egyszerű vizualizáció például itt.
[7]. Az orvosi vizsgálatok másik kategóriáját a kísérletes vizsgálatok jelentik, ahol mód van randomizációra, tehát, hogy véletlenszerűen sorsoljuk ki, hogy ki kap oltást és ki nem. Ennek pont az a lényege, és legnagyobb előnye, hogy ilyen módon biztosan nem lesz semmilyen szisztematikus különbség a két csoport között az oltottság tényén túl, ezért ha találunk különbséget a kimenetben, akkor az biztosan az oltás miatt lesz (és a véletlen ingadozás miatt, de az kezelhető statisztikai eszközökkel). Azaz, legalábbis elvileg, mentesek tudunk lenni a confounding-tól! Ez a kísérletes vizsgálatok hatalmas előnye, sajnos azonban cserében több hátrányuk is van.
[8]. Kiegészítő függelék, S1-es táblázat.

2.2.2. Ez azért is érdekel minket, mert az általunk ismert angol statisztika szerint egyáltalán nem az oltatlanok voltak a legnagyobb veszélyben a járványidőszak alatt.

De. Az alábbi ábra mutatja a már hivatkozott – és a nyílt levélben is szereplő – angol adatok szerint a koronavírus ellen valaha is oltottak (ever vaccinated) és az oltatlanok (unvaccinated) bármely okból bekövetkező halálozási rátáit:

Mint látható, az oltatlanok kockázata minden egyes hónapban magasabb, mint az oltottaké.

A kérdésben szereplő félreértés oka talán az lehet, hogy az oltottaknak vannak olyan alcsoportjaik, amelyekben magasabb a halálozás, mint az oltatlanoknál (például: csak 1 oltást kapott, de több mint 21 napja). Ezek a csoportok azonban már benne vannak a „valaha oltottak” halmazában, tehát amikor azt mondom, hogy az oltottak kockázata alacsonyabb, akkor az azt jelenti, hogy még ezekkel az alcsoportokkal együtt is alacsonyabb.

Mindazonáltal a következőkben bemutatom, hogy miért kell óvatosnak lenni az ilyen alcsoportokra vonatkozó adatok értelmezésével. Amint láttuk, bármi is jön ki egy ilyen vizsgálatból, abból nem lehet az oltás hatására következtetni: a fenti grafikon sem jelenti önmagában azt, hogy az oltás jót tett, és ha pont fordított eredményt kaptunk volna, az sem jelentené, hogy rosszat. Ezt a problémakört az alcsoportokra lebontás sajnos csak felerősíti: az előbbi állítás oka az volt, hogy az oltottak és az oltatlanok csoportja eltérhet egymástól az oltottság tényén túl egyéb jellemzőikben is, márpedig ez a probléma hatványozottabban fog jelentkezni akkor, ha még az oltottakon belül is speciális csoportokat nézünk, mint mondjuk hogy „csak 1 oltást kapott, de több mint 21 napja”. Ilyen értelemben tehát akit nem érdekelnek ezek a részletek, az teljes nyugalommal átugorhatja a most következő részt e magyarázat mellett, de talán mégsem felesleges ezt megbeszélni, mert ennek a végiggondolása egyúttal az egész kérdéskör, a confounding jobb megértését is elősegíti.

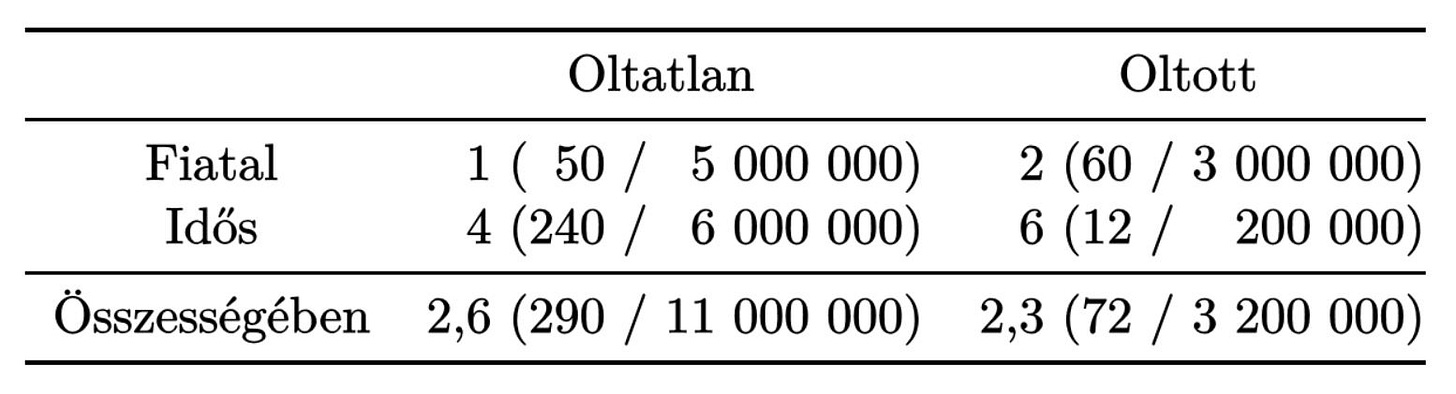
Ahhoz, hogy mindezeket megbeszéljük, először a standardizálás fogalmával kell megismerkedni. Ez a varázsszó már szerepelt az ábrán, az angolok ezt használták, de vajon mi ez egyáltalán, és miért volt rá szükség? Hadd szemléltessem a dolgot egy nagyon egyszerű, illusztratív példán. Egy országban 11 millió oltatlanból 290 halt meg adott időintervallum alatt (2,6 / 100 ezer fő halálozási ráta), a 3,2 millió oltott közül 72 (2,3 / 100 ezer fő halálozási ráta). Minden más problémát félretéve, mit tudunk mondani az oltás hatásáról? Ez látszólag szinte nevetségesen nyilvánvaló kérdés: jótékony a hatása, hiszen a 2,3 kisebb, mint a 2,6. Mi itt egyáltalán a kérdés?

Nos, az, hogy a helyzet lehet bonyolultabb. Nem biztos, hogy az, lehet, hogy tényleg jótékony az oltás, csak épp lehet ez is:

A táblázatban a zárójelen belül az adott csoportból kikerült elhunytak száma van elosztva a csoport létszámával, a zárójel előtt pedig az osztás eredményeként kapott halálozási ráta szerepel (/100 ezer fő mértékegységben).

Először is, ellenőrizzük le, hogy stimmelnek a számok: 50 + 240 az tényleg 290, 5 + 6 millió az tényleg 11 millió és így tovább. Tehát stimmel a dolog, tényleg lehet ez a helyzet a fent felvázolt szituáció háttérében.

Igen ám, de ha jobban megnézzük, akkor itt valami nagyon furcsa! Eredetileg azt mondtuk, hogy az oltás jótékony, viszont itt azt látjuk, hogy a fiatalok körében is káros (1 helyett 2 / 100 ezer fő a halálozási arány), és az idősek körében is káros (4 helyett 6 / 100 ezer fő). Micsoda? – kérdezheti valaki. Ez meg hogy lehet? Hogyan fordulhat elő, hogy valami ebben a csoportban is káros, abban is káros, összességében meg jótékony?! Néhányan akár azt is gondolhatják, hogy ez lehetetlen, mármint nem infektológiailag, hanem egyenesen matematikailag, de nem az – erre a fenti táblázat a bizonyíték, ha valaki nem hiszi el, adja össze és ossza el a számokat!

Mi történik itt? Ha jobban megnézzük a táblázatot, hamar összerakhatjuk a képet: az oltás valóban ront a helyzeten minden életkor mellett, viszont a fiatalabb életkor meg – nem meglepő módon – javít (4-ről 1-re, illetve 6-ról 2-re), és közben az a helyzet, hogy az oltottak sokkal fiatalabbak összetételükben, mint az oltatlanok. Egyszerűen az történik, hogy az oltottak átlagosan fiatalabb életkora többet javít, mint amennyit az oltottságuk ront! Ez a magyarázat a látszólag paradox helyzetre.

Először is állapítsuk meg, hogy ez a confounding egy példája! (Valójában a talán legegyszerűbb példája.) A probléma az, hogy összehasonlítunk két csoportot, oltottakat és oltatlanokat, de azok nem csak az oltottság tényében térnek el. Ahogy korábban is volt róla szó, ilyenkor nem fogjuk tudni biztosan, hogy ha találunk is eltérést az eredményben, jelen esetben a halálozásban, az mi miatt van; ez a példa annyival több, hogy itt megadtam a tényezőt is, amiben még eltér a két csoport, ez volt az életkor. Az ilyen változót szokták egyébként confounder-nek, magyarul zavaró változónak hívni.

Adja magát a kérdés, hogy ha [9] ismerjük a zavaró változót, akkor tudunk-e valamit tenni a torzító hatásának megszüntetéséért? A válasz az, hogy igen: ennek az egyik klasszikus módszere a standardizálás.

Az alapötlet a következő. Az 1 és 2, illetve a 4 és 6 számok rendben vannak, azok mutatják a valódi helyzetet (hogy ti. az oltott csoportban nagyobb a halálozás). A baj a 2,6-tal és a 2,3-mal van. De hogyan jöttek ezek ki? Érdemes végiggondolni, hiszen a 2,6 nyilván nem független az 1-től és a 4-től, azokból jött ki valahogy. És csakugyan: a 2,6 nem más, mint az 1 és 4 súlyozott átlaga, ahol a súly az életkor szerinti megoszlás az adott csoportban! Az oltatlanok körében ez a megoszlás úgy néz ki, hogy 45% fiatal (5/11), 55% idős (6/11), és valóban: 0,45 · 1 + 0,55 · 4 = 2,6! Hasonlóképp, az oltott csoportban a kormegoszlás 94% fiatal, 6% idős, és csakugyan: 0,94 · 2 + 0,06 · 6 = 2,3.

Tehát: a fiatalok és idősek körében kiszámolt értékkel nincs gond, a gond az, hogy nagyon különböző korfával rakjuk őket össze egy számba! Ha így nézzük, akkor adja magát a megoldás: számoljuk ki fiatalokra és idősekre a halálozási arányt, majd rakjuk őket össze egy számba – csak épp ugyanazt a korfát használva mindkét csoportban! Legyen például ez az egyezményes korfánk – szokás referencia, vagy standard populációnak is hívni – az, hogy 80% fiatal, 20% idős. Ezzel összerakva az oltatlan csoport adatait azt kapjuk, hogy 0,8 · 1 + 0,2 · 4 = 1,6, az oltottakra pedig 0,8 · 2 + 0,2 · 6 = 2,8. Rendben vagyunk! Ezzel a módszerrel helyes eredményt kaptunk: egyetlen összefoglaló számba sűrítettük a halálozást így is, ugyanúgy, mint a rossz módszernél, csakhogy így már helyes eredményeket kaptunk, látszik, hogy az oltott csoportban rosszabb a helyzet. Ezt a módszert szokás standardizálásnak, az így kapott rátát pedig standardizált halálozási rátának nevezni.

Az (életkorra történő) standardizálás során lényegében az történik, hogy az életkort, mint zavaró változót kikapcsoljuk. (Mást persze nem, ennek később nagy jelentősége lesz.) A standardizált ráta használata azért fontos, az angolok is ezért alkalmazták, mert így legalább egy eltéréssel kevesebb van a csoportok között: legalább az nem torzítja a csoportok közti összehasonlítást, ha az életkori összetételük eltérő.

Most, hogy értjük a standardizálás mibenlétét és működését, nekiállhatunk felfejteni az angol adatokat! A kérdéskört matematikai képletek helyett egy példán keresztül szeretném bemutatni, melyen végigkövethető, hogy mi történik. A példa illusztratív, a számokat hasból adtam meg úgy, hogy szép kerekek legyenek, de azért nem véletlenszerűek: úgy választottam meg, hogy visszaadják az angol adatok néhány fontos jellemzőjét (amin a kérdéskör is múlik).

Kezdjük azzal, hogy egyszerűsítjük a képet, az angol adatokban ugyanis 7 életkori csoport és 10 oltottsági kategória van. A valódi számításokhoz tényleg fontos, hogy minél finomabb felbontásunk legyen, mivel azonban mi most amúgy is csak illusztrációt gyártunk, ez inkább hátrányos lenne, hiszen nagyon nehezen áttekinthetővé tenné a példát. Ezért egyszerűsítsünk: csak háromféle oltottsági kategóriát fogok használni (oltatlan, 1-3 dózist kapott, 4 dózist kapott), és mindössze kétféle életkori csoportot, hívjuk őket az egyszerűség kedvéért „idős”-nek és „fiatal”-nak.

Ennyi felvezetés után nézzük az adatokat! Az alábbi táblázat mutatja a példám számait; minden cellában zárójelen belül az adott csoport halálozásainak száma van elosztva a csoport létszámával [10], a zárójel előtt pedig az így kialakuló halálozási ráta látható, /100 ezer fő/év-ben megadva:

Első lépésben standardizáljuk az adatokat, hogy összehasonlítható összefoglaló számokat nyerjünk! Legyen a használt standard korfánk [11] a következő: fiatal 80%, idős 20%. Ekkor például az 1-3 oltást kapottak standardizált halálozási rátája: 0,8 · 300 + 0,2 · 6000 = 1440. Hasonlóképp végigszámolva a többit a következő eredményt nyerjük:

A helyzet tehát világos: az oltatlanok kivétel nélkül minden csoporthoz viszonyítva jobb eredményt produkálnak, mint az oltottak! Vegytiszta, egyértelmű eredmény.

Vagy mégsem? Az első dolog ami gyanús lehet, hogy mi történik akkor, ha valaki véletlenül kiszámolja, hogy mi a helyzet általában az oltottakkal, tehát, ha nem törődünk azzal, hogy hány oltást kapott, nem különböztetjük ezeket meg, egyszerűen azt nézzük, hogy kapott-e oltást vagy sem. Ez könnyen megtehetjük: fiatalból van az oltottak között 300 + 15 = 315 halálozás és 100000 + 1000 = 101000 emberév utánkövetés, így a ráta 315/101000 = 312. Idősebbeknél ugyanez 600 + 300 = 900 halálozás és 10000 + 10000 = 20000 emberév utánkövetés, így 900/20000 = 4500 a ráta; ezekkel a standardizált érték 0,8 · 312 + 0,2 · 4500 = 1150. Na de álljunk meg! 1150? Nézzünk rá egy pillanatra újfent az előbbi táblázatra: ez jobb, mint bármelyik ott szereplő érték!

Ez két szempontból is rettentő furcsa első ránézésre. Először is, akkor mégis az oltottak állnak jobban? Hiszen az előbb még azt állapítottuk meg, hogy az oltatlanok…! A másik furcsaság: hogyan lehet 1150 az oltottak együttes értéke, ha a két csoportjuk külön-külön 1440 és 1800? Hogy lehet együttvéve kisebb, mint bármely csoportjuk…?

A választ kezdjük azzal, hogy bármennyire is furcsának tűnik, de a helyzet tényleg ez – ha valaki nem hiszi el, kapjon elő egy számológépet, és üsse be! De akkor hogyan történhet ez meg?

A magyarázat egyik kulcseleme a 4 oltást kapott fiatalok. Ha jobban megnézzük, akkor azt látjuk, hogy ők nagyon kevesen vannak ugyan, viszont rendkívül rossz halálozási rátával bírnak (ötszöröse a halálozásuk, mint az 1-3 oltást kapott fiataloknak, négyszerese, mint az oltatlanoknak). Ez teljesen reális, ugyanezt tapasztaljuk a valóságban is: ha valaki fiatal kora ellenére mégis sok oltást kapott, akkor jó eséllyel krónikus beteg, hiszen pont azért kapott sok oltást, mert valamiért úgy ítélték meg, hogy nagy kockázatnak van kitéve az életkora ellenére is. (Angliában konkrétan ma már az újabb dózisokat fel sem ajánlják [12] 75 év alatt, ha az ember nem immunkárosodott.) Nem meglepő tehát, hogy nekik nagyon rossz a halálozásuk.

Rendben, de miért olyan fontos ez az ügy, ha egyszer úgyis kevesen vannak? Akkor a végeredményt sem fogják nagyon befolyásolni! – gondolhatná az ember, csakhogy ez nem így van. A standardizálás ugyanis azt jelenti, hogy a fiatalok adata mindenképp 80%-os súllyal számít, bármennyien vannak is! Nézzük meg a 4 oltást kapottak korfáját: kevesebb, mint 10%-uk fiatal, de a standardizált rátában az ő – nagyon rossz – adataik mégis 80%-os súllyal fognak számítani! Emiatt hiába vannak nagyon kevesen, a 4 oltásos csoport összesített eredményét rendkívül lehúzzák, így jön ki az 1800.

Mindeközben az oltottaknak általában nem rossz az eredményük a fiatal korosztályban, ami nem is meglepő, hiszen 100 ezer kis halálozású fiatal van a mindössze 1000 nagyon rossz halálozású mellett – csakhogy, és itt jön a második csavar, ez nem tud érvényesülni ha külön-külön számolunk, hiszen ilyenkor mindkét értékben ugyanúgy 80%-os súlya lesz a fiatalkori adatnak, az sehol nem jelenik meg, hogy a kis halálozásúak 100-szor többen vannak, mint a rossz halálozásúak! Nem is jelenhet, hiszen elkülönülve számoltunk. Lényegében az történt, hogy egy 101 ezer fős csoport nagyon jó (és oltatlanokénál is jobb!) 312-es eredményt szétszedtük olyan aszimmetrikus módon, hogy abból egy 300-as és egy 1500-as csoport képződött – majd utána mindkettőnek 80%-os súlyt adtunk a saját számításában, függetlenül attól, hogy az utóbbi csak 1000 emberből számolódott, az előbbi meg 100 ezerből. Pontosan ugyanez történt az idősebbeknél, csak kicsit kevésbé drámai formában, ahol egy 4500-as (oltatlanokénál szintén jobb!) eredményt szedtünk két részre. Így jött létre a felvázolt helyzet.

Ez a jelenség magva elméleti szinten, hátra van még, hogy mindezeket a gyakorlatban is igazoljam. (Igazolás alatt természetesen nem azt értem, hogy „biztosan így történt a valóságban”, pláne, hogy az állításom pont az, hogy mi sem tudhatjuk, hogyan történt, hanem azt, hogy lehetséges, hogy így történt. Ezt viszont teljeskörűen meg fogom mutatni.) Két dolgot is szeretnék igazolni: az egyik, hogy a krónikus betegek egyenetlen eloszlása tényleg meg tudja magyarázni a fenti eredményeket, a másik, hogy – persze pont ebből fakadóan – tényleg teljesen fals eredményt is kaphatunk az oltásra vonatkozóan, ha ilyen típusú adatokból próbálunk következtetni úgy, hogy közben nincs információnk a zavaró változókról, és nem tudunk korrigálni rájuk.

A bizonyítást a következő táblázat jelenti:

Igen, ez az egyetlen táblázat, amiben mindössze annyit csináltam, hogy az adatokat lebontottam krónikus betegség szerint [13], igazolja a fenti állítást. Hogy miért? Azért, mert ha megnézzük jobban, akkor kiderül, hogy ez a táblázat igazából az előző táblázat! Pontosabban szólva egy lehetséges táblázat annak háttérében. Nézzük meg: az előző táblázat szerint a 100 ezer 1-3 oltást kapott fiatal körében 300 halálozás volt – itt pontosan ez van, hiszen 30 + 270 = 300 és 70000 + 30000 = 100000. Ha végigmegyünk az összes rovaton, akkor látjuk, hogy mindegyik stimmel, kiadja összegként az előző táblázat számait.

Tehát, kijelenthetjük, hogy elvileg lehet, hogy ez áll az előző táblázat hátterében. Rendben, de ez miért olyan nagyon érdekes? Azért, mert… nézzük csak meg az oltatlanok hogyan viszonyulnak az oltottakhoz! Mi a helyzet a fiatal, nem krónikus beteg emberek körében? Itt az oltatlanok produkálják a legrosszabb halálozást (59 nagyobb, mint 43 és mint 0). Na és a fiatal, krónikus betegek körében? Szintén, 2000 nagyobb, mint 900 és mint 1667. És az idős, nem krónikus betegek? Itt is az oltatlanok halálozása a legrosszabb (2800 nagyobb, mint 2500 és mint 2000). Na, és az idős, krónikus betegek? Itt is az oltatlanok halálozása a legrosszabb, 7200 nagyobb, mint 6875 és mint 4000.

Azaz: az oltatlanok minden esetben rosszabb eredményt produkálnak, mint az oltottak – és ez az eredmény minden további nélkül lehet annak a hátterében, hogy az oltatlanok minden esetben jobb eredményt produkálnak, mint az oltottak! (Mert emlékezzünk vissza, ebből a mondatból indultunk ki néhány bekezdéssel ezelőtt!) Ezt a fenti táblázat igazolja – ha valaki nem hiszi, adja össze a számokat!

Zárásként újra hangsúlyozom, hogy azt természetesen én sem tudom, hogy valóban ez van-e az adatok mögött. De pont ez a lényeg, épp ez az állításom: hogy nem tudjuk – de lehet ez is. Az oltottak rosszabb adata mögött lehet az, hogy az oltás rosszat tesz, de lehet az is, hogy az oltás kimondottan jót tesz (ezt igazoltam a fentiekben), meg persze lehet a kettő között bármi. Ezt mi magunk sem tudhatjuk, pont ezért mondtam, hogy az ilyen jellegű adatokból nem lehet az oltás hatásosságára vagy biztonságosságára vonatkozó következtetést levonni. Ez természetesen nem azt jelenti, hogy szerintem nem kell vizsgálni ezt a kérdést, nagyon is kell – csak alkalmas módszerrel. Ez nem az.

Lábjegyzet:
[9]. A ,,ha” szócska nagyon fontos. Bármit is csinálunk, csak akkor tudjuk megtenni, ha van információnk a zavaró változóról, aminek persze az is előfeltétele, hogy eszünkbe jusson, hogy az egy zavaró változó. Mi van, ha nem jut eszünkbe, hogy eltér a két csoport között az életkor eloszlása? Mi van, ha eszünkbe jut, de nincs információnk az emberek életkoráról? A kísérletes vizsgálatoknak pont ez a nagy előnye, hogy olyan confounder-ek ellen is védelmet nyújtanak, amikről nincs információnk, sőt, azok ellen is, amikről eszünkbe sem jutott, hogy confounder-ek!
[10]. Valójában itt nem létszámról kellene beszélni, hiszen az egyes emberek utánkövetési ideje nem biztos, hogy azonos volt. Az epidemiológusok erre használják az emberév fogalmát: ha egy embert egy évig követünk után az egy emberév. Tehát ha 2 embert 1 évig követünk az 2 emberév, de az is 2 emberév, ha 1 embert 2 évig követünk, vagy 4-et 0,5 évig és így tovább. Elvileg tehát ezzel kell osztani, de ha valaki ezt kényelmetlennek találja, nyugodtan gondolhatja úgy is, hogy ez a létszám, csak akkor hozzá kell képzelnie, hogy mindenkit pont ugyanannyi ideig követtünk után.
[11]. Ez nagyjából megfelel annak, mintha az Európában legáltalánosabban használt – és az angolok által is alkalmazott – ún. ESP2013 standardban 65 évnél húznánk meg az ,,idős” határát. Ez nyilván nagyon durva felbontás, de a dolognak nincs jelentősége, hiszen ahogy mondtam is, ez amúgy is csak illusztráció, a valódi vizsgálatokban sokkal finomabb korfát kell használni; az angolok is ezt tették.
[12]. Itt elolvashatóak a legutóbbi kampány szabályai, itt pedig megtalálható (3. és 4. táblázat), hogy ki minősül krónikus betegnek, ideértve az immunszuppressziót is.
[13]. Hasonlóan az ,,idős” – ,,fiatal” felosztáshoz, természetesen ez is idézőjeles, hiszen az emberek nem oszhatóak ilyen egyszerűen ,,krónikus beteg” – ,,nem krónikus beteg” kategóriákba. Sokféle krónikus betegség lehetséges, akár még a súlyosságuk is számíthat; itt most egyszerűsítettem, hiszen úgyis az a cél, hogy egy áttekinthető példát kapjunk.

2.2.3. Hogyan könyveljük el ezeket az adatokat? Van rájuk valami olyan magyarázat, ami alapján egyértelműen nem kell ezekkel foglalkoznunk, vagy további vizsgálatok folynak ezen irányokban? Ha igen, mik?

Az adatokkal kapcsolatban az egyik problémát, a confounding-ot, az előbbiekben már kifejtettem. Itt most egy másik problémakört említenék még meg: azt, hogy ez a bármely okból bekövetkező halálozásokat mutatja. Ennek vitathatatlanul van egy előnye is, jelesül, hogy mind az oltás esetleges hasznának, mind az oltás esetleges kárának a biztosan teljes megragadását jelenti, hiszen az eredmény nem függ a haláloki besorolástól. A gond az, hogy cserében van egy nagyon súlyos hátránya: az, hogy a mutatót „hígítják” az irreleváns halálesetek. A bármely okból bekövetkező halálozásokban ugyanis minden benne van villámcsapástól az autóbalesetig, amelyeket sem nem okoz, sem nem előz meg az oltás. Ha ilyen irreleváns esetekkel felhígítjuk a két csoportot, az elmossa a valódi különbséget, lényegében egy zajt jelent, amely mellett sokkal nehezebb lesz észrevenni az esetleges jelet. Egy tomboló járvány közepén, ahol a halálesetek érdemi részét maga a járvány okozza, ez talán nem akkora gond, de járványon kívül, amikor a halálesetek túlnyomó többsége irreleváns lesz, ez pláne baj. (Ha most visszanézünk az angol ábrára, azonnal érthető, hogy miért csökken folyamatosan a két csoport közötti különbség – még ha el is tekintünk a confounding-tól.)

A helyzetet tovább rontja, hogy a két problémakör kölcsönösen felerősíti egymás hatását: a confounding miatt különösen a kis különbség értelmezése lesz lehetetlen, hiszen az végképp nyugodtan kijöhet az eltérő összetételből, a bármely okú halálozás pedig csökkenti a különbség mértékét.

Végeredményben tehát azt kapjuk, hogy ezek az adatok szinte használhatatlanok, akár az oltás hatásosságát, akár a biztonságosságát vizsgálnánk. Kényszerből elfogadható lehet olyan helyzetben, ahol nincs jobb adat (mondván, hogy ha valami nagyon kiugró van, legalább azt észrevegyük), de ahol rendelkezésre állnak finomabb, egyéni szintű adatok alapján kontrollált vizsgálatok, ahogy a koronavírus elleni oltás esetében rendelkezésre állnak, ott azok szolgáltatnak sokkal megbízhatóbb információkat.

3. Ön mit gondol: jól mértük fel a járványidőszakban a veszély léptékét?

3.1. Milyen arányban voltak a „Covid áldozatok” között azok, akik „Coviddal” és nem „Covid miatt” haltak meg? Mi ennek a jelentősége?

E kérdés megválaszolásához elsőként definiálnunk kell, hogy mit értünk egyáltalán „Coviddal” és „Covid miatt” történő elhalálozáson.

Az első meglehetősen egyértelmű: a beteg úgy halt meg, hogy közben koronavírus-fertőzött volt. Ennek hazánkban nagyjából [14] megfelel a napi gyorsjelentésben közölt halálozás-szám. A második kérdés bonyolultabb, hiszen egy haláloki besorolási algoritmust igényel, szerencsére erre van egy standardizált, nemzetközileg is egységes, és – a mai betegségosztályozási rendszerével – több mint 30 éve használatban lévő eljárás [15], mely alapján Magyarország is osztályozza a halottvizsgálati bizonyítványokat, meghatározva a halálokot.

Ezeket a definíciókat használva a következő táblázat mutatja évente lebontva a napi gyorsjelentésben kimutatott [16], és a halottvizsgálati bizonyítvány szerinti [17] koronavírusos halottak számát Magyarországon:

A fentiek alapján tehát a válasz a kérdésre: nagyjából 86%-os arányban. E szám jóságának megítéléséhez vegyük figyelembe, hogy a napi gyorsjelentés közléséhez átlagosan 12 óra áll rendelkezésre, a halottvizsgálati bizonyítványokból származó halálokok közléséhez pedig 8 hónap.

Lábjegyzet:
[14]. E kitételt azért voltam kénytelen beszúrni, mert Magyarországon – szégyenszemre – a járvány egész ideje alatt nem közöltek semmiféle esetdefiníciót, hogy egyáltalán mi alapján történik a besorolás. Más országokban ennek volt egy – természetesen nyilvánosan közölt – eljárásrendje. Ez mindenképp elfogadhatatlan véleményem szerint, de látni fogjuk, hogy e konkrét kérdésben nem igen befolyásolja az eredményt.
[15]. A Központi Statisztikai Hivatal kézikönyve elérhető itt, az Egészségügyi Világszervezet kézikönyve pedig itt.
[16]. Az adatforrás a jól ismert https://koronavirus.gov.hu/-val egyező adatokat közlő, de jelenleg is elérhető WHO COVID-19 dashboard.
[17]. Akinél az elsődleges halálok a Betegségek Nemzetközi Osztályozásának 10. revíziója szerinti U071.0, U072.0, U09.9 vagy U10.9 kód. Az adatforrás az Egészségügyi Világszervezet Mortalitási Adatbázisa. Egyszerűbb lekérdezését, vizsgálatát lehetővé teszi a https://research.physcon.uni-obuda.hu/OkspecifikusMortalitasiAdatbazis/ címen elérhető weboldalam.

6. Ön szerint a többlethalálozási adatok a járványügyi intézkedéseink (pl.: lezárások, oltások) sikereit vagy sikertelenségét bizonyítják?

Szerintem egyiket sem, és ami még fontosabb, hogy azért nem, mert nem is bizonyíthatják. Félreértés ne essék, fontos ezeket az adatokat monitorozni, az eredményeket tanulmányozni, mert hasznos észrevételeket tehetünk (a következő pontban igyekszem erre konkrét példákat is mutatni!), de bizonyítékot, pláne erős bizonyítékot, ne várjunk az ilyen adatoktól. Különösen, ha egyszerűen csak az éves többlethalálozásokat nézzük.

A probléma itt is a confounding, csak a szereposztás más: itt most nem emberek különböző csoportjait, hanem különböző időszakokat vagy különböző országokat hasonlítunk össze – de a gond ugyanaz, az összehasonlított időszakok, illetve országok nem csak az összehasonlítás tárgyában térnek el. Innentől kezdve, ha találunk is különbséget a kimenetben, nem tudhatjuk, hogy az mitől, melyik eltéréstől van. 2020 és 2022 nem csak abban tér el, hogy az egyik alatt volt oltás, a másik alatt meg nem, Dánia és Magyarország nem csak abban tér el, hogy az egyikben magasabb az átoltottság, a másikban alacsonyabb. Hanem nagyjából egymillió dologban – ha találunk is különbséget, nem tudhatjuk, hogy az az oltástól, a maradék egymillió eltérés valamelyikétől, vagy esetleg ezek valamilyen keverékétől volt.

Ez után pedig mindent megismételhetnék amit korábban mondtam, csak a szavakat kell lecserélni. A magasabb átoltottságú országokban alacsonyabb a többlethalálozás, akkor ez bizonyítja, hogy az oltás hatásos? Fene tudja, mi van, ha a magasabb átoltottságú országokban egyúttal kevesebb a krónikus beteg, és ez a valódi oka az ottani jobb adatoknak? Itt is érdemes az alternatív megfogalmazásra gondolni: lehet, hogy alacsony a többlethalálozás, de mi van, ha oltás nélkül még alacsonyabb lett volna? (Nem ismerjük a „mi lett volna ha” forgatókönyvet.) Természetesen a dolog fordítva is igaz: az oltás bevezetése után megnő a többlethalálozás, akkor ez bizonyítja, hogy az oltás hatástalan vagy egyenesen káros? Fene tudja, mi van, ha az oltás bevezetése utáni időszakban egyúttal egy új variáns is megjelent és ez a valódi oka a rosszabb adatoknak? Avagy, megint csak: lehet, hogy magasabb a többlethalálozás, de mi van, ha oltás nélkül még magasabb lett volna?

6.1. Az OECD többlethalálozási adatai szerint [LINK] sok országban nem 2020 vagy 2021, hanem 2022 volt a leghalálosabb. Ilyen volt például Németország, Franciaország, Ausztria, Izrael, Dánia, Finnország, Norvégia, Kanada, Ausztrália, Új Zéland, de a legjobban beoltott Chile és Portugália többlethalálozási adatai sem tűnnek megnyugtatónak. Ez miért lehet?

Az előző pontban kifejtetteken túl itt felhívnám még egy szempontra a figyelmet, jelesül, hogy ebbe a listába elég sok olyan ország is bekerült, ahol már az adatok „2022 volt a leghalálosabb” típusú tálalása (és az oltásra való célzás) önmagában is megkérdőjelezhető, és akkor még az interpretációról nem is beszéltünk.

Nézzük meg [18] ezeket kicsit részletesebben!

Kezdjük Dániával; az alábbi ábra mutatja a többlethalálozást (és megjeleníti a jelentett koronavírus-halálozást is):

Az ábra máris sokkal jobban kontextusba helyezi a „2022 volt a leghalálosabb” állítást. Először is állapítsuk meg, hogy annak, hogy 2022 volt Dániában a leghalálosabb, egyetlen oka van: az, hogy valami történt az év végén. Ez a valami nem valószínű, hogy az oltástól, a lezárások pszichológiai hatásaitól vagy akár az elmaradt kezelések miatt történt, hiszen ezek egyike sem olyan halálozást okozna, ami több mint egy évvel később két hét alatt felfut, de nagyon, majd újabb két hét után szinte a nullára esik vissza.

De akkor mi történt? Az időzítés, valamint épp a felfutás és visszaesés gyorsasága miatt nem nehéz kitalálni: ezt a valamit úgy hívják, hogy influenza! Egész egyszerűen az történt, hogy Dániának 2022/23 telén volt egy komoly influenza-járványa, aminek a 2022-re eső része lerontotta a 2022-es adatot.

Hozzáteszem, azt, hogy a koronavírus-járvány után újult erővel fog jönni az influenza, előre lehetett tudni [19]: a járvány alatt két influenza-szezon is elmaradt a védelmi intézkedések pozitív indirekt hatásaként (kijárási tilalom alatt az influenza sem tud jól terjedni), de ez – és ezt már akkor lehetett tudni – bizonyos értelemben vissza fog ütni, ugyanis az influenza elleni védettségben fontos komponens, hogy a szezonális járványok alatt sokan szereznek valamilyen szintű immunitást évről-évre. Ha ez kiesik, pláne ha többször is egymás után, az azt jelenti, hogy a következő télnek a szokásosnál jóval alacsonyabb immunitással fogunk nekivágni.

Visszatérve Dániára, annak, hogy egyetlen influenza-járvány is ennyire le tudta rontani a 2022-es adatokat, hogy az a leghalálosabb év lett, két oka van. A kézenfekvő magyarázat, hogy Dánia olyan jól védekezett a koronavírus-járvány alatt, annyira kevés többlethalálozása lett, hogy ahhoz képest már egyetlen influenza-járvány is el tudott rontani egy évet. Ez kétségtelenül igaz, de ha mélyebbre ásunk, akkor van még egy tényező. Ha egy pillanatra visszanézünk most az ábrára, feltűnhet, hogy mind 2020, mind 2021 elején van egy negatív csúcs a többlethalálozásban. Mi történt akkor? Hogyan lehet, hogy ennyire kevesen haltak meg ott, legalábbis a többlethalálozás szerint? A helyzet az, hogy a válasz megint csak az influenza! Ugyanis a többlethalálozás számítása során használt várható halálozási adatban benne van az influenzaszezon (hiszen azok a múltbeli adatokon alapszanak, amiben ott van a téli influenza). Vagyis amikor 2020-ban, illetve 2021-ben elmaradt az influenza, akkor a várható halálozás kivonása során levontunk valamit (az influenza-szezon halottjait), amit nem kellett volna levonni, hiszen nem is volt influenza! Ez a levonás okozza a negatív csúcsot [20]. Azaz: abban, hogy 2022 lett a legrosszabb Dániában, nem csak az van benne, hogy 2022 rossz volt, hanem az is, hogy 2020 és 2021 mesterségesen jó lett, a szükségtelenül kivont influenzás halottak miatt!

Pontosan ugyanez figyelhető meg a felsorolt országok közül vegytisztán Németországban, Franciaországban és Ausztriában, kevésbé tisztán Norvégiában:

Továbbmenve, Ausztrália és Új-Zéland nem is igazán értem hogy került fel a listára: igen, 2022 volt a legrosszabb év – na de oda a járvány is csak akkor ért el érdemben! A nullához képest nem akkora csoda, hogy rosszabb lett az eredmény…

Zárásként hangsúlyozom, hogy nem azt mondom, hogy a felvetett kérdés nem fontos, vagy hogy nem kell vizsgálni, hanem azt, hogy ezekből az adatokból nem lehet. A kérdés fontos, kell vizsgálni – ideértve a vakcina hatását is – de ezt csak úgy lehet megtenni, ha értjük az adatok limitációit és kontextusát, ezek sokszor egyáltalán nem nyilvánvalóak, ismerjük az elemzésük lehetséges módszereit, azok előnyeit és hátrányait, ez alapján megfelelő megközelítést választunk, és tisztában vagyunk a levonható következtetések bizonyítóerejével. Az ezt figyelmen kívül hagyó elemzésekkel nem az a bajom, hogy sajnálom, hogy vizsgálják a kérdést, hanem az, hogy nem segítik a válaszok megtalálását.

Lábjegyzet:
[18]. A vizsgálat során nem az OECD – nyílt levélben hivatkozott – többlethalálozási adatait fogom használni, hanem a World Mortality Dataset (WMD) számait. A dolognak hatalmas jelentősége nincsen, nagy különbségek nincsenek a kettő között, de az OECD metodikája nem a legszerencsésebb, mert egyszerűen a múltbeli évek átlagait veszi. Ez nem jó módszer akkor, ha a mortalitásnak hosszú távú trendje van – mint ahogy a legtöbb országban van – mert így növekvő trend esetén alá-, csökkenő trend esetén fölébecsüljük a várható halálozás-számot. A WMD ennél ügyesebben jár el (lásd: Ariel Karlinsky, Dmitry Kobak. Tracking excess mortality across countries during the COVID-19 pandemic with the World Mortality Dataset. Elife. 2021 Jun 30:10:e69336.), mert a trendet hosszabbítja meg. Ha valakit részletesebben érdekelnek a többlethalálozás számítási módszertanának kérdései, merem ajánlani a https://github.com/tamas-ferenci/ExcessMortEUR címen elérhető írásomat.
[19]. Íme egy 2021 közepi cikk, ami előre megmondta, hogy erre készülni kell:
Erik A Karlsson, Piers Andrew Nicholas Mook, Katelijn Vandemaele, Julia Fitzner, Aspen Hammond, Vanessa Cozza et al. Review of global influenza circulation, late 2019 to 2020, and the impact of the COVID-19 pandemic on influenza circulation. Weekly Epidemiological Record, 2021, 25: 241-264.
[20]. Ha valaki nem éven belüli ingadozást is mutató görbét néz, hanem éves adatot, az felfoghatja úgy, hogy a levont várható halálozásban benne van egy ,,átlagos influenza-évadnyi halott”, amit levontunk, pedig nem kellett volna.

Remélem, hogy a fentiekkel hozzá tudtam járulni a felvetett kérdések kapcsán zajló diszkusszióhoz!

Ferenci Tamás

Ferenci Tamás válaszait olvashattátok. Hamarosan újabb válaszokat teszünk fel.

KORONATANÚK

Discussion about this post